|
|
|
Click on each of following figures to watch a larger view.
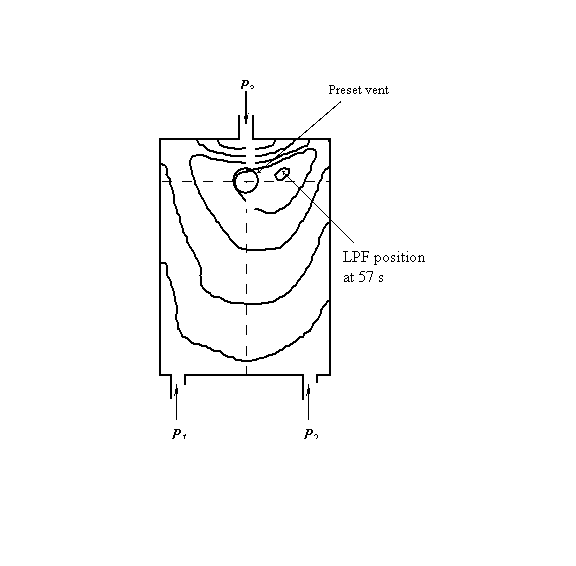 Fig 1.
Fig 1.
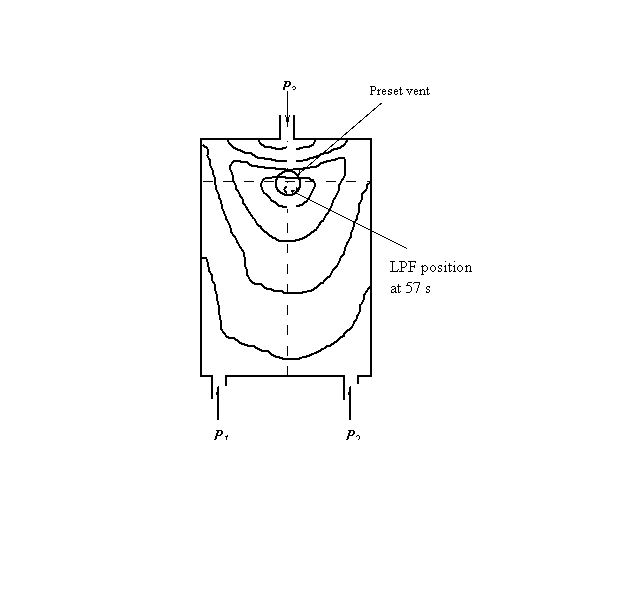 Fig 2.
Fig 2.
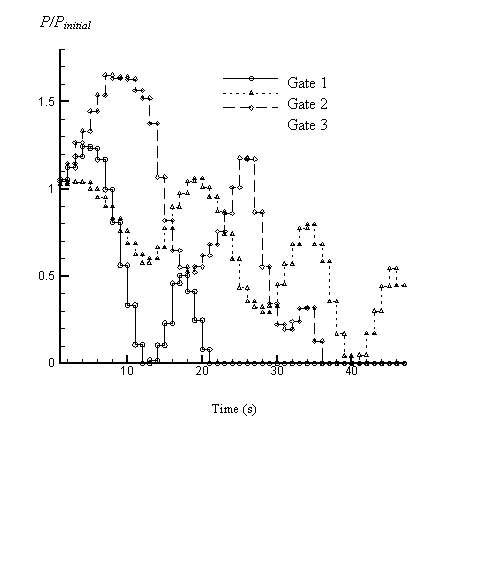 Fig 3.
Fig 3.
Fig. 1 Filling front positions and the Last Point to Fill (LPF) position
that does not coincide with the preset vent location without control
Fig. 2 Filling front positions and the LPF position that coincide
with the preset vent location with control
Fig. 3 The history of injection gate pressures achieving Fig. 2 under control
To top
Click on each of following figures to watch a larger view.
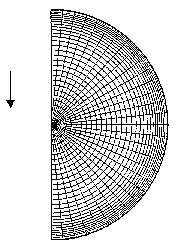 Fig 1.
Fig 1.
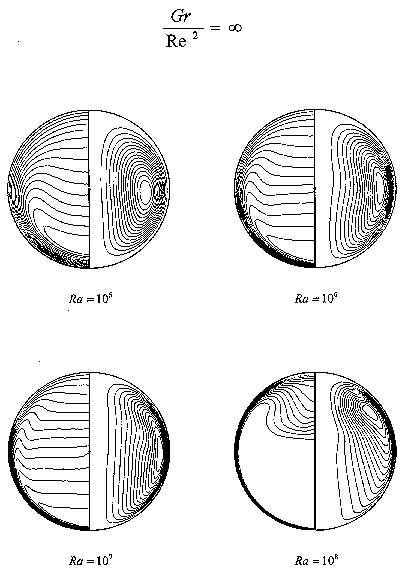 Fig 2.
Fig 2.
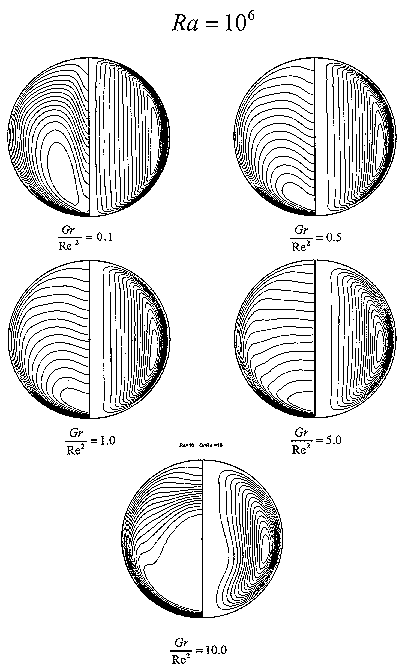 Fig 3.
Fig 3.
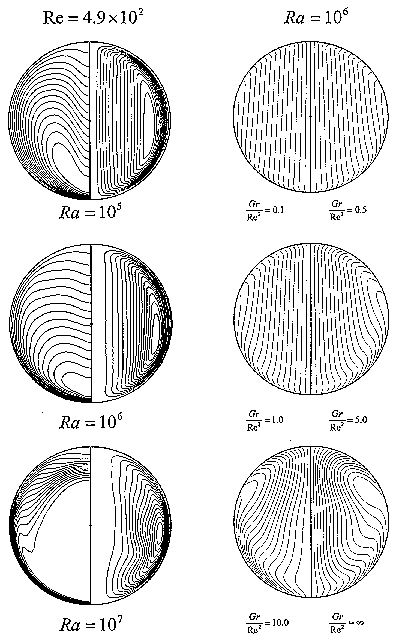 Fig 4.
Fig 4.
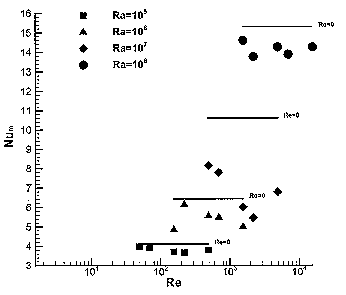 Fig 5.
Fig 5.
Fig. 1 Schematic diagram of the computational grid system
Fig. 2 Pseudosteady-state streamline patterns and temperature field contours
corresponding to the Rayleigh number 105, 106,
107, and 108 within non-rotating spheres
Fig. 3 Pseudosteady-state streamline patterns and temperature field contours
corresponding to the Rayleigh number of 106 (Gr/Re2
=0.1, 0.5, 1, 5 and 10)
Fig. 4 Left coloum Pseudosteady-state streamline patterns and
temperature field contours corresponding to Re=4.9 × 102
(Ra=105,106 and 107)
Right coloum Pseudosteady-state streamline patterns and
temperature field contours corresponding to Re=106
(Gr/Re2= 0.1, 0.5, 1, 5, 10 and ¥)
Fig. 5 Dependence of the mean Nusselt number on the Rayleigh and Reynolds numbers
To top
Click on each of following figures to watch a larger view.
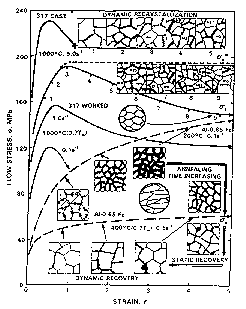 Fig 1.
Fig 1.
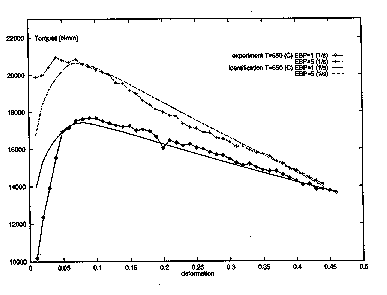 Fig 2.
Fig 2.
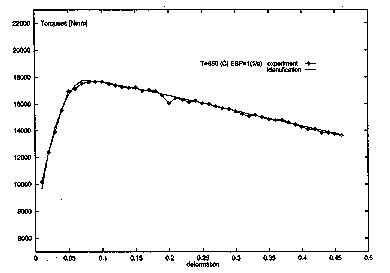 Fig 3.
Fig 3.
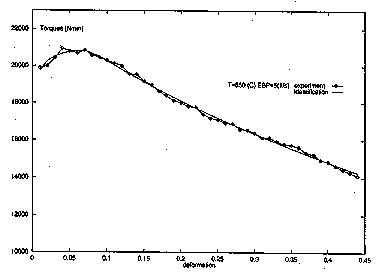 Fig 4.
Fig 4.
 Fig 5.
Fig 5.
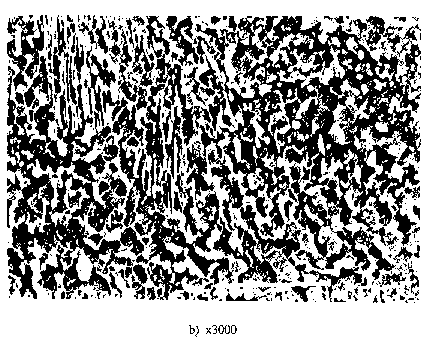 Fig 6.
Fig 6.
 Fig 7.
Fig 7.
Fig. 1 Flow curves corresponding to DRV (dash lines) and DRX (solid lines)
(Curtesy of J.J. Ionas et al, Treastise on Materials Science and Technology,
Vol. 6, Plastic Deformation of Materials, 394-490. Academic Press, New York, 1975)
Fig. 2 Torque versus deformation of experiment and calculation at 650°
C and nominal strain rates of 1 s-1 and 5 s-1
Fig. 3 Torque versus deformation of experiment and calculation at 650°
C and nominal strain rates of 1 s-1
Fig. 4 Torque versus deformation of experiment and calculation at 650°
C and nominal strain rates of 5 s-1 (Notice that when identification is performed
separately at strain rates of 1 s-1 (Fig. 3) and of 5 s-1 (Fig. 4),
the agreement is better than that obtained from identifying both simultanuously (Fig. 2))
Fig. 5 Simulation result of temperature distribution with constitutive equation proposed and parameters
identified at nominal strain rate of 5 s-1
Fig. 6 Microstructure of XC70 ([C]=0.65 - 0.73) after deformation at boundary area of the sample
Fig. 7 Size of substructure distribution simulated according to a formula proposed in the research
To top
Click on each of following figures to watch a larger view.
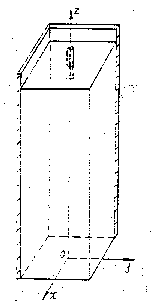 Fig 1.
Fig 1.
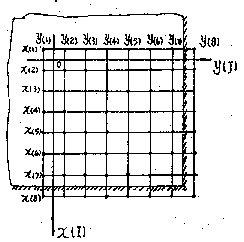 Fig 2.
Fig 2.
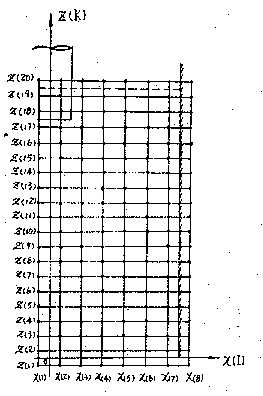 Fig 3.
Fig 3.
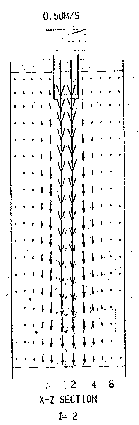 Fig 4.
Fig 4.
 Fig 5.
Fig 5.
 Fig 6.
Fig 6.
 Fig 7.
Fig 7.
Fig. 1 Computational domain (a quarter of the mold)
Fig. 2, 3 Computational grids
Fig. 4 One of the 2-D views of the folw fields from the simulations
Fig. 5 Experimental setup for the flow field measurement with LDA
Fig. 6 Snapshot of the flow field corresponding to Fig. 4
Fig. 7 The flow field from LDA corresponding to Fig. 4
Click on each of following figures to watch a larger view.
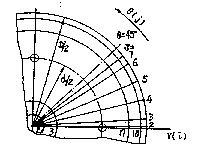 Fig 1.
Fig 1.
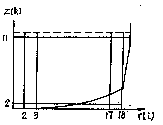 Fig 2.
Fig 2.
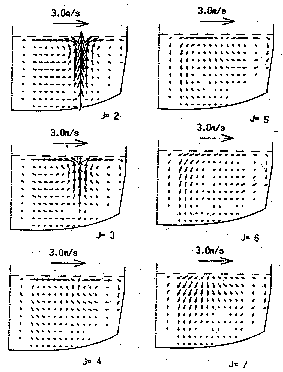 Fig 3.
Fig 3.
Fig. 1, 2 Computaional grids
Fig. 3 Velocity field from the simulation
Click on each of following figures to watch a larger view.
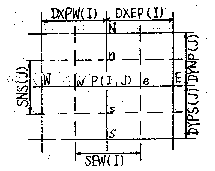 Fig 1.
Fig 1.
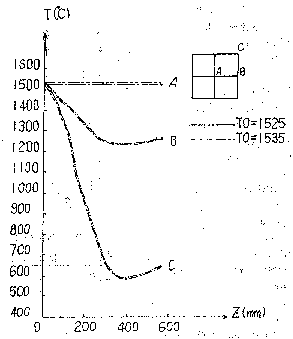 Fig 2.
Fig 2.
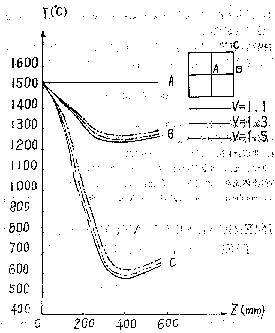 Fig 3.
Fig 3.
Fig. 1 A control volume used in the calculation
Fig. 2 The effect from the temperature of the liquid metal in the tundish on the
temperature distribution inside the mold
Fig. 3 The effect of withdrawal rate on the temperature distribution inside the mold
Click on each of following figures to watch a larger view.
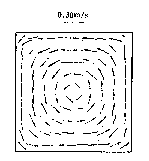 Fig 1.
Fig 1.
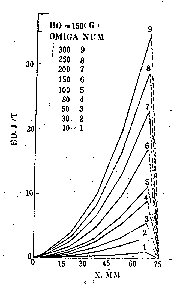 Fig 2.
Fig 2.
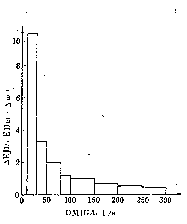 Fig 3.
Fig 3.
Fig. 1 One of the simulated flow patterns under SEMS
Fig. 2 The effect of one operational factor from SEMS on the flow
Fig. 3 Relative change of flow energy versus the change of one operational factor
To top